Kunci Jawaban Matematika – Di bawah ini jawaban dari latihan Matematika kelas 9 yang ada pada halaman 115 dan 116, yang berfokus pada pemahaman tentang fungsi kuadrat. Para siswa kelas 9 SMP diharapkan dapat menyelesaikan sepuluh soal esai yang terkait dengan konsep fungsi kuadrat tersebut.
Materi mengenai fungsi kuadrat dipelajari dalam Bab 2 mengenai Persamaan dan Fungsi Kuadrat dalam kurikulum pelajaran Matematika untuk kelas 9 SMP.
Disarankan bagi para siswa untuk terlebih dahulu memahami materi sebelum merujuk kepada kunci jawaban Matematika kelas 9 yang ada pada halaman 115 dan 116.
Berikut kunci jawaban Matematika kelas 9 halaman 115 116
Baca juga :Kunci Jawaban Bahasa Indonesia Kelas 9 Halaman 28 Semester 1, Kurikulum Merdeka
KUNCI JAWABAN
Soal nomor 1
Diketahui rumus (a)x2+(b)x+c
maka:
Titik (-1,1)
1 = a(-1)2 + b(-1) + c
1 = a – b + c
Titik (0,-4)
-4 = a(0)2 + b(0) + c
-4 = c
Titik (1, -5)
-5 = a(1)2 + b(1) + c
-5 = a + b + c
Maka subsitusinya adalah:
1 = a – b – 4
a – b = 5
dan
-5 = a + b – 4
a + b = -1
Jadi
a – b = 5
a – (-3) = 5
a = 2
2 + b = -1
b = -3
Sehingga diperoleh
y = ax2 + bx + c,
y = 2×2 – 3x – 4
Soal nomor 2
Memotong sumbu-X pada titik (4, 0) dan (–3, 0) adalah
y = a (x – x1)( x –x2)
y = a (x – 4)(x + 3)
Dengan melewati (2, -10) diperoleh:
-10 = a (2 – 4)(2 + 3)
-10 = a (-2)(5)
-10 = -10a
a = -10/-10 = 1
y = 1(x – 4)(x + 3)
Jadi y = x2 – x -12
Baca Juga : Kunci Jawaban Soal Seni Budaya Kelas 9 Halaman 27 K13: Seni Patung
Soal nomor 3
Diketahui p = 2 dan q = -16
Jika melalui puncak (p,q)
Maka y = a(x – p)2 + q
y = a(x – 2)2 – 16 melalui (x, y) = (-2, 0)
0 = a (-2 – 2)2 – 16
0 = a (16) – 16
-16 a = -16
a = 1
Jadi fungsi kuadratnya adalah
y = 1 (x – 2)2 – 16
y = x2 – 4x + 4 – 16
y = x2 – 4x -12
Soal nomor 4
Diketahui f(x) = ax2 + bx + c
Maka:
f (0) = 4
f (0) = a(0)2 + b(0) + c
a(0)2 + b(0) + c = 4
0 + 0 + c = 4
c = 4
Subtitusi sumbu simetri x didapatkan dari:
-b/2a
-b/2a = 2
-b = 4a
b = -4a
Substitusi pada fungsi
f(x) = ax2 + bx + 4
f(x) = ax2 – 4ax + 4
f(-1) = -1
f(-1) = a(-1)2 – 4a(-1) + 4
a(-1)2– 4a(-1) + 4 = -1
a – 4 (-1) a + 4 = -1
a + 4a + 4 = -1
5a + 4 = -1
5a = -5
a = 1
Jadi bentuk fungsi dari f(x) = ax2 + bx + c adalah
f(x) = ax2 – 4ax + 4
f(x) = (-1)x2 – 4(-1)x + 4
f(x) = -x2 + 4x + 4
Soal nomor 5
Fungsi kuadrat yang grafiknya melalui (12, 0), (0, 3), dan (0, –2) maka:
x = a(y – y1) (y – y2)
x = a(y – 3) (y – (-2))
x = a(y – 3) (y + 2)
12 = a (0 – 3) (0 + 2)
12 = a (-3) 2
12 = -6a
a = -2
Jadi
x = a(y -3) + (y + 2)
x = -2 (y – 3) (y + 2)
x = -2 (y2 + 2y – 3y – 6)
x = -2 (y2 – y – 6)
x = -2y2 + 2y + 12
Soal nomor 6
DIketahui f(x) = ax2 + bx + c
Maka a.02 + b.0 + c = p
c = ax2 + bx + p
Jika grafik melalui (p, 0) dan (–p, 0), maka f(p) = 0 dan f( -p) = 0
f(p) = ap2 + bp + p = 0
= ap + b + 1 = 0
= ap – b + 1 = 0
2b = 0
b = 0
dan
ap2 – bp + p = 0
ap – b + 1 = 0
ap + 1 = 0
a = -1/p
Jadi f(x) = -1/p x2 + p
Baca Juga : Kunci Jawaban Matematika Kelas 10 Halaman 40 dan 41 Latihan 2.1 Barisan Aritmetika Kurikulum Merdeka
Soal nomor 7
Diketahui y = x2 – 5x + 4, y = x – 1
Maka:
x2 – 5x + 4 = x – 1
x2 – 5x – 1 + 4 + 1 = 0
x2 – 6x + 5 = 0
(x – 5)(x – 1) = 0
x = 5 atau x = 1
Sehingga subtitusinya y = x – 1 Atau y = x – 1
y = 5 – 1 y = 1 – 1
y = 4 y = 0
Jadi titik potongnya adalah (5,4) dan (1,0).
Soal nomor 8
Diketahui y = x2 – 6x + 4 , y = x2 – 8x.
Maka:
x2 – 6x + 4 = x2 – 8x
x2 – x2 – 6x + 4 = -8x
-6x + 4 = -8x
2x = -4
x = -2
Sehingga subtitusinya diperoleh
y = x2 – 8x
y = -22 – 8(-2)
y = 4 + 16
y = 20
Jadi titik potongnya adalah (-2, 20).
Soal nomor 9
Diketahui y = x2 – 4x + 2, y = ax + b, tepat di koordinat (3, –1)
Maka:
y = ax + b
-1 = a(3) + b
-1 = 3a + b
b = -1 – 3a
x2 – 4x + 2 = ax + b
x2 – 4x – ax + 2 – b = 0
x2 – (4 + a) x + 2 – b = 0
Jadi
a = 1
b = -(4 + a)
c = 2 – b
0 = b2 – 4ac
0 = (-(4 + a))2 – 4(1) (2 – b)
0 = 16 + 8a + a2 – 8 + 4b
0 = a2 + 8a + 4b + b
Diperoleh substitusi b = -1 – 3a
a2 + 8a + 4b + 8 = 0
a2 + 8a + 4(-1 – 3a) + 8 = 0
a2 + 8a – 4 – 12a + 8 + 0
a2 – 4a + 4 = 0
(a – 2)2 = 0
a – 2 = 0
a = 2
b = -1 – 3a
b = -1 – 3(2)
b = -7
Jadi, nilai :
a = 2
b = -7
Soal nomor 10
Diketahui y = 2×2 – 12x + 16
Maka dari y = ax2 + bx + c diperoleh
a = 2, b = -12, c = 16
y = 0
y = 2×2 – 12x + 16
0 = 2×2 – 12x + 16
0 = (2x – 4)(x – 4)
2x – 4 = 0 atau x – 4 = 0
2x = 4 atau x = 4
x = 2 atau x = -4
(2, 0) atau (4,0)
Sumbu simetri x
x = -b/2a
x = – (-12) / 2(2)
x = 3
Sumbu simetri y
y = b2 – 4ac / – 4a
y = (-12)2 – 4(2)(16) / – 4 (2)
y = 144 – 128 / -8
y = 16 / -8
y = -2
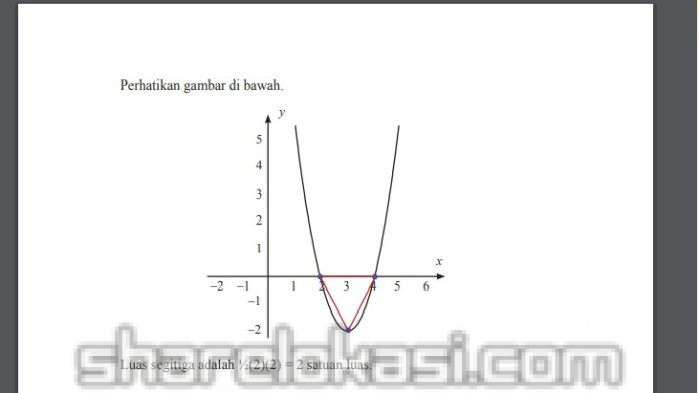
Maka titik puncaknya adalah (3, -2).
Gambarnya adalah sebagai berikut: